Autor:	Burkhard Heim
Keywords:	Physik, Einheitliche Quantenfeldtheorien, Materie, Elementarstrukturen,
Abstract:	Eine kurze übersichtliche Einführung in das Werk von Burkhard Heim.
Copyright:	Copyright der Texte: Burkhard Heim, Northeim, 1998 Copyright der HTML-Gestaltung: Bernhard Harrer, Berlin, 1999
Info Jockey's Comment:	This article has also been published in english language.  Einen Text wie diesen in HTML darzustellen ist leider noch immer nicht einfach. Deshalb freut es mich besonders, im Folgenden diesen faszinierenden Artikel von Burkhard Heim präsentieren zu können. [IJBH]

	28. Jul. 1999
	Übersicht Burkhard Heim  Datadiwan Netzwerk

Um in der Physik zu einer umfassenden, einheitlichen Theorie zu gelangen, die möglichst viele phänomenologische Erscheinungsformen beschreibt, gibt es verschiedene Möglichkeiten.

Als eine dieser Wege wäre hier die Geometrisierung physikalischer Strukturen zu nennen, der in den beiden Bänden "Elementarstrukturen der Materie" [1] und [2] beschritten wurde. Der Vorteil liegt offensichtlich in der Tatsache, daß hier der Raum und das Ding nicht mehr wesensfremd sind, sondern, daß das Ding nunmehr als spezifische metrische Struktur dieses Raumes erscheint. Eine Konsequenz ist dabei die Einheit von Feld und Feldquelle. Der erste Versuch einer solchen Geometrisierung, und zwar des Gravitationsfeldes, wurde von A. Einstein in der allgemeinen Relativitätstheorie unternommen und später von Kaluza, Klein, Penrose und P. Jordan u.a. weitergeführt.

Als Nachfolge des Kaluza-Klein Modells können die Supergravitations- und Superstringtheorie erwähnt werden. Gegenwärtig wird die Superstringtheorie weiter entwickelt, weil man hofft in einem R₁₀ die 4 empirisch bekannten Wechselwirkungen einheitlich beschreiben zu können. Allerdings bleibt unbekannt, wie die für Partikelenergien von ca. 10¹⁸ GeV gültigen Aussagen dieser Theorie in den tatsächlich meßtechnisch erfaßbaren Bereich der Hochenergiephysik zu transferieren sind. Hier scheint der in [1] und [2] beschriebene Weg einer radikalen Geometrisierung zu geeigneteren Ergebnissen zu führen, die unmittelbar mit der Praxis vergleichbar sind.

Einen völlig anderen Zugang zu einer Vereinheitlichung der Naturbeschreibung ergiebt sich aus gruppentheoretischen Überlegungen. So erzielte man einen gewissen Erfolg mit der Symmetrieuntersuchung einer U(1)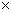SU(2) , die es ermöglicht, die schwache und die elektromagnetische Kraft einheitlich zu beschreiben. 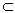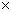Für die starke Kraft gilt eine SU(3), so daß für die Vereinheitlichung mit der schwachen und der elektromagnetischen Wechselwirkung der Standardtheorie entsprechend, eine SU(5)U(1)SU(2)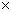SU(3) erforderlich wäre. Schließlich sollte die Superstringtheorie auch das Gravitionsfeld beschreiben, was durch eine SO(32) bzw. E8 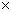E8 möglich wird. Ein empirischer Nachweis für diese Theorien konnte noch nicht erbracht werden, zumal die Terme von Massenspektren (auch im Rahmen der Supergravitation) in einem viel zu hohen Energiebereich liegen. Darüber hinaus fehlen Aussagen über allgemeine Quantenzahlensätze (wiederum im Sinne von Spektren) denen die Massenterme als Resonanzspektren einschließlich ihrer oberen Grenzen zugeordnet sind.

In Weiterführung der Gedanken von Einstein, Kaluza und Klein, aber auch von Jordan wurde nicht nur das Gravitationsfeld, sondern auch die übrigen Kraftfelder als Strukturen der Raumzeit R₄ (als Minkowskiraum mit x₄=ict) mit typischen Invarianzen geometrisiert. Auf diese Weise ergibt sich dann jedoch im R₄ eine allgemeine nichthermitische Geometrie, deren Dreizeigersymbole in den kovarianten Komponeneten zwar in einen hermitischen und einen antihermitischen Anteil spaltbar sind, die aber im Gegensatz zu einer Riemannschen Geometrie allgemein nicht explizit durch Ableitung der Komponenten des Strukturtensors darstellbar sind, es sei denn man führt Zusatzbezeichnungen ein, von denen jedoch nicht bekannt ist ob sie (als Einschränkung der Allgemeinheit) physikalisch überhaupt zulässig sind. Es müssen also diese Dreiziegersymbole als Komponenten eines einheitlichen Strukturfeldes behandelt werden.

Wird nach dem Korrespondenzprinzip ein Übergang in den Mikrobereich vorgenommen, dann zeigt sich, daß diese einheitlichen Feldkomponeneten zu echten gemischtvarianten Tensorkomponenten i.B. auf die allgemeine Poincaré-Gruppe werden. Für den Makrobereich gilt dies auch, weil man für ein Strukturfeld (seinen Invarianten entsprechend) immer nur ein geodätisches System auffinden kann, nicht aber für die übrigen Felder; denn jedes dieser Strukturfelder wird durch spezifische Invarianzforderungen, also andere Geodäsiebedingungen gekennzeichnet.

Beim Übergang der in den kovarianten Indizierungen nichthermitischen 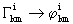 in den Mikrobereich werden also die 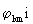zu den gemischtvarianten Komponenten eines Tensorfeldes für die 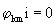nur im Fall der völligen Strukturfreiheit des betreffenden R₄-Bereiches erreichbar ist. Die phänomenologische Energiedichte wird im Mikrobereich zu Diskontinuitäten 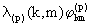 die metrischen Strukturstufen äquivalent sind. Es bedeutet (p), daß für diesen Index die Summenkonvention nicht gilt. Diese Geometrisierung des Energiedichtebegriffes erscheint deshalb, weil phänomenologische Energien als Zeitänderungen von Wirkungen ein, also räumliche Energiedichten letzlich raumzeitliche Wirkungsdichten sind, so daß wegen des Quantenprinzips der Wirkungen ein Limes zum Differentialquotienten nicht möglich ist. Aus diesem Grunde muß eine geometrische Letzteinheit existieren.

Betrachtet man die nichtlinearen und nichthermitischen Zustandsgleichungen der R₄-Struktur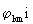, dann fallen algebraische Symmetrien auf, die aussagen, daß von den insgesamt 4³=64 Beziehungen für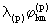 stets 28 leer bleiben, so daß 36 zu  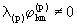werden, während die leeren Strukturstufenspektr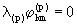en wegen 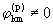 für die 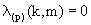bedingen. Da die Strukturstufen im Mikrobereich Äquivalente zu phänomenologischen Energiedichtediskontinuitäten sind, müssen die von 0 verschiedenen Komponeneten eine Tensorschema bilden, welches wegen ihrer Anzahl 36 nur sechsreihig sein kann. Nach der Tensorgeometrie bedingt dies aber einen R₆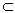R₄ als Bezugsraum. Dies bedeutet noch keinen Widerspruch zur Kopenhagener Schule; denn x₅ und x₆ sind ebenso imaginär wie x₄.

Möglicherweise könnte auch J. v.Neumann den aus pragmatischen Gründen definierten Begriff der Quantentheorie etwas zu eng gefaßt haben. Schließlich sind Raum und Zeit des R₄ nur die Kategorien menschlicher Anschauung (nach I. Kant). Es wäre hier zu bemerken, daß die R₆-Koordinaten auf Grund von Erhaltungssätzen energetisch definiert sind, so daß der Bezugsraum R₆ als solcher der materiellen Welt aufzufassen ist, wobei x₅ und x₆ als organisatorische Koordinaten materieller Strukturen (in R₄) zu interpretieren sind.

Ein Existenznachweis der 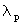zeigt, daß die 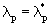 als Eigenwerte tatsächlich existieren, doch erscheint dabei eine weitere Symmetrie, die aufzeigt, daß von den 36 Komponenten des Energiedichtetensors im Makrobereich noch einmal 12 Komponenten verschwinden, wobei es sich um die 4× 3 raumartigen Komponenten der doppelten Ränderung des R₄-Abschnittes handelt. Dies ist hinsichtlich der makrophysikalischen Empirie durchaus verständlich. Andereseits ergab sich hieraus das Bildungsgesetz möglicher Hyperraumdimensionen.

Sind empirisch 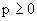 Dimensionen eines  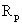vorgegeben, dann existiert mit den positiven ganzen Zahlen  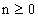ein Bezugsraum 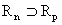, wenn neben der Ganzzahligkeit von 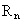 die Bedingung

(n-1)²-1=p(p-1)(p-2) erfüllt ist. Für p=0...2 folgt n=2 für den positiven und n= 0 für den negativen Zweig, doch ist dieser Zweig fürp>2 nicht relevant. Schließlich ist die Bedingung für p=3 ebenso wenig erfüllt wie für p= 5 und allep>6. Für p=4, also die Raumzeit ergibt sich hingegen tatsächlich n=6, doch existiert für die materielle Welt 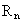 mit p=6 ein Hyperraum n=12, so daß  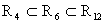gilt. Der in R₆ definierte Energie- bzw. Materiebegriff ist in den ebenfalls imaginären Koordinaten x₇...x₁₂ nicht mehr definiert, wohl aber der Volumenbegriff. In den Bänden [1] und [2] wird in halbklassischer Form nur die materielle Welt R₆ diskutiert, weil die nichtlinearen und nichthermitischen R₄-Beziehungen in den R₆ übertragen werden können, wobei dann allerdings eine völlige Hermitezität erscheint.

Zur Herleitung der erwähnten notwendigen geometrischen Letzteinheit muß ein universelles Hintergrundphänomen betrachtet werden, als welches sich die allgemeine Trägheit jeglicher Energiemasse anbietet, die nach einem Äquivalenzprinzip stets Gravitationsphänomenen äquivalent ist. Aus einer in [1] entwickelten phänomenologischen Gravitationsdynamik kann eine skalare Feldfunktion 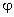 durch einebenfalls nichtlineares phänomenologisches Gleichungssystem beschrieben werden, das formal mit den nichtlinearen Strukturbeziehungen im R₆ übereinstimmt, so daß die Beziehung für 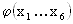 im Fall einer Konstanz hinsichtlich  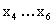zur R₃-Beziehung  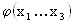wird.

Da 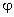 als gravitatives Beschleunigungsniveau (Quadrat einer Orbitgeschwindigkeit) stets positiv und reell, also lm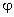=0 bleibt, kann die nichtlineare Differentialgleichung unter der Voraussetzung sphärischer Symmetrie 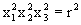 gelöst werden. Die implizierte Lösung (als (11) in [1] angegeben) zeigt, daß das relle Feld j nur zwischen den beiden Realitätsschranken R_- und R₊ existiert. Hier entsprechen R_- dem Schwartzschild- und R₊ dem Hubbleradius. Im Bereich geringer Abstände (Planetensystem) wird 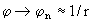 praktisch dem Newtonschen Gesetz identisch, doch ändert sich dies im Bereich großer Entfernungen, weil es eine Grenze des attraktiven Gravitationsfeldes 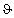 gibt, die zwischen R_- und R₊ liegt, aber durch den Kubus des mittleren Atomgewichts A der Feldquelle gemäß 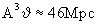 abhängt.

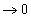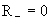Wird das Feld nur einer Elementarkorpuskel betrachtet, dann kommt zu diesen charakteristischen Entfernungen R₊ und R_- noch die Compton-Wellenlänge hinzu. Im Leerraum (die Masse der Feldquelle ) verschwindet , während 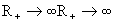 ebenso divergiert wie  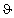oder die Compton-Wellenlänge. Eine geometrische Letzteinheit t muß als reele Zahl und Leerraumeigenschaft in 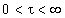liegen. Dies trifft jedoch nur für ein einziges Produkt dieser charakteristischen Längen zu, was in (15) aus [1] als Flächenelement 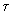=m² stets geodätisch begrenzt den numerischen Wert 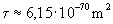 liefert. In [1] wurde daher (Kapitel III) ein Differenzkalkül des als Metron bezeichneten Elements 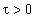 entwickelt, welches gestattet irgendeinen infinitesimal ausgedrückten Sachverhalt mit 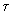 zu metronisieren, wobei jeder Unterraum R_n der Welt durch  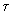bestimmt wird, wenn nMOD2=0 ist, was für den R₆ ebenso erfüllt ist wie für den R₁₂. Auf diese Weise konnte als im nichtlinearen System der R₆-Strukturen 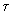 im Sinne eines Differentialkalküls berücksichtigt werden.

Da die 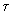 stets geodätisch begrenzt, aber als Flächeninhalte konstant sind, beschreibt die metronisierte Zustandsfunktion sozusagen eine relative Kondensation der metronischen Elemente einer Struktur bei ihrer Projektion in einen euklidischen Bezugsraum, die in einer schwachen Analogie zu den Höhenlinien einer Gebirgskarte Aufschluß über die projezierte Struktur geben kann. Hier scheint eine gewisse Analogie zu den Regge-Polen oder den topologischen Untersuchungen von H. Jehle vorzuliegen. Das Metronische Gleichungssystem selbst hat den Charakter eines Auswahlprinzips, welches aus der mehrfach unendlichen Schar möglicher R₆-Strukturen diejenigen auswählt, die, in den R₄ projeziert, materielle Elementarprozesse in der physischen Welt beschreibt.

Eine weitere Analyse zeigt, daß es für diesen "Weltselektor" 4 Lösungsmanigfaltigkeiten gibt, die sich auf die Unterräume S₂(x₅, x₆) der Organisation, T₁(x₄) der Zeitstruktur und R₃(x₁, x₂, x₃) des physischen (hinsichtlich der Drehgruppe kompakten) Raumes beziehen.

Bei diesen Lösungen handelt es sich um die Strukturen a:S₂, ferner um 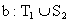 sowie 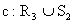 und 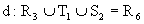. Die Menge der R₆ Koordinaten wird also strukturiert mit dem Kardinalzahlenkomplex {3;1;2}=K₆. Der organisatorische Strukturanteil 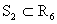 begleitet also alle Elementarstrukturen.

Zur Interpretation der Formen a bis d wird eine Art "Hermeneutik der Weltgeometrie" erforderlich, so daß a bis d kurz als "Formen der Hermetrie" bezeichnet werden können. Bei a handelt es sich um Strukturen außerhalb des R₄, die allgemein nicht physikalisch interpretierbar sind, aber in R₄ projeziert als Gravitonenfeld erscheinen. Die Elemente der Form b haben als Weltlinien nur Gerade im Asymptotenkonus des zweischaligen Hyperbelraumes (R₄) und bewegen sich daher grundsätzlich mit Lichtgeschwindigkeit im R₃; deshalb sind sie als Photone zu interpretieren. Die Hermetrieformen c und d werden durch die Einbeziehung der rellen Einheit R₃ gekennzeichnet, was im Gegenstz zu a und b ihre Ponderabilität, also eine Ruhemasse bedingt. Es sind c als neutrale und d als elektrisch geladene Korpuskeln zu interpretieren. Bei d scheint die Form b mit c gekoppelt zu sein, wobei die Kopplung den Ladungszustand kennzeichnet. Es ergab sich eine einfache Darstellung einer durch das Quantenprinzip bedingten elektrischen Elementarladung, deren numerischer Wert allerdings um 0,125% vom Meßwert der Elektronenladung abweicht.

Auch kann ein allgemeines Massenspektrum hergeleitet werden, doch liegen seine Terme praktisch so dicht, daß ein Kontinuum angenähert wird. Dies geht allein darauf zurück, daß die energetischen Terme aller Hermetrieformen superponieren, d.h., daß dem praktisch kontinuierlichen Spektrum der Imponderablen a- und b-Terme die Punktspektren der c- und d-Hermetrie überlagert sind. Zur Seperation dieser Punktspektren wird als ein Termselektor erforderlich. Immerhin können die unteren Schranken der c- und d-Spektren ermittelt und durch allgemeine Naturkonstanten dargestellt werden. Es handelt sich um die kleinsten wägbaren Massen einer R3-Struktur, wobei sich für d die Elektronenmasse und für c eine um ca. 0,1% unter der Elektronenmasse liegende neutrale Masse ergiebt.

In [2] wird gezeigt, daß die obere Realitätsschranke eines Gravitationsfeldes mit abnehmender Feldquelle steigt, d.h. für die kleinstmögliche Ruhemasse ergibt sich ein Maximalwert R_max, so daß 2R_max=D die größtmögliche Distanz im R₃ ist, die in [2] als Universumsdurchmesser definiert wurde, aber allein von elementaren Naturkonstanten abhängt. Substituiert man mit 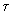 nach (15) in [1], dann verschwinden diese Konstanten in der Beziehung und es verbleibt ein algebraischer Ausdruck höheren Grades für die Abhängigkeit D(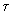 ), der als kosmologische Beziehung (37) mit (37a) in [2] Bezeichnet wurde. Aus astrophysikalischen Gründen ist für die zeitliche ÄnderungD>0 zu setzen, was 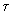<0 zur Folge hat. Geht man in der zeitlichen Vergangenheit zurück, nimmt D ab, während 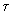 ansteigt.

Dies hat ein Ende wenn 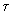 als 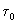 ein "Protouniversum" D₀ umschließt, also  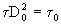gilt. Da 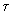nicht unterschreitbar ist, liegt hier ein Eckereignis des R₄ vor, für welches es keine Vergangenheit mehr gibt, so daß dies Ereignis als Zeitpunkt t=0 des kosmogonischen Ursprungs definiert wurde. Mit einer geeigneten Substitution nimmt D(t ) die Gestalt eines Galois-Polynoms 7. Grades an , das für t=0 und nach Überschreitung eines Maximalwertes D_max und einer Kontraktionsphase D<0 bei t=0<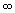, also dem Ursprung t=0 und der Endzeit t= sechs relle Lösungen im Sinn von 2 Sphärendreiheiten und eine Komplexe Lösung hat. Im offenen Intervall 0<t< gibt es hingegen nur eine relle Lösung. Bei der Aktualisierung kosmischer Bewegung von t= 0in t>0 beginnt die ExpansionD>0 in einem zeitlichen Nacheinander der kosmischen Sphären, was wesentlich später (wahrscheinlich im Intervall der Materiekosmogenie) nach einem Symmetriebruch globaler Gruppen die Entstehung von 3 Struktureinheiten 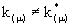 im Sinne tensorieller Kerne von Integraloperatoren zur Folge hat. Dies bedingt nach dem metronischen Differenzkalkül durch Iteration 2. Grades Strukturtensoren allgemein nichthermitischer partieller Art.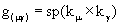

Nach den 4 Hermetrieformen a bis d können diesen 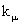die Abhängigkeiten von den hermetrischen Unterräumen des R₆ gemäß k₁(S₂) sowie k₂(T₁) und k₃(R₃)zugeornet werden. Auf diese Weise entstehen zunächst 9 Partialstrukturen einer Eneametrie der Hermetrieform d, aber für k₍₂₎=E die raumartige Hexametrie der Form c sowie für k₍₃₎=E eine zeitartige Hexametrie der Form b, während sich für k₍₂₎= k₍₃₎=E die Pseudobimetrie der Hermetrieform a ergibt. Die polymetrischen Partialstrukturen 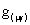 komponieren dabei zum hermiteschen Strukturfeld des ebenfals hemiteschen Kondensors. Aus diesem Grunde kann sowohl der Weltselektor als auch das Kondensorfeld in diesen Partialstrukturen gespalten werden, so daß für jede Hermetrieform ein System partieller Strukturen entsteht, was in der Lösung des allgemeinen Energiespektrums bei richtiger Wahl der Strukturindizierungen (mg ) eine Speparation der Punktspektren c und d entspricht. Die Lösungen liefern dann tatsächlich Punktspektren ponderabler Massenterme, die recht gut mit den Partikel- und Resonanzspektren verglichen werden können, die im Rahmen der hochenergiephysikalischen Empirie nachgewiesen und in ihren Eigenschaften gemessen wurden.

Hinsichtlich der von der Hochenergiephysik experimentell beschriebenen Elementarkorpuslen ergiebt sich aus dieser theoretischen Analyse folgendes Bild:

Die ponderablen (also mit Ruhemasse versehenen) Elementarpartikel sind Selbstkopplungen freier Energie, die i.B. auf die Eigenschaft der Ruhemasse durchaus als elementar angesehen werden können, aber dennoch durch eine sehr subtile Internstruktur dynamischer Art gekennzeichnet sind. Der Begriff "elementar" ist also zu relativieren.

Tatsächlich erscheint eine solche Korpuskel als ein elemntares Flußsystem (äquivalent zu Energieflüssen) im R₆, welches aus ureinfachsten dynamischen Elementen (Protosimplexe) aufgebaut ist. Die Existenzbedingung fordert, daß die Zyklizität während mindetsens einer Flußperiode gewahrt bleibt, so daß die Zeitspanne während derer die Partikel stabil sind stets durch das ganzzahlige Vielfache der Flußperiode ausgedrückt wird. Jede mögliche dynamische Struktur (als Flußaggregat) des R₆ wird dabei durch einen Satz aus 6 Quantenzahlen beschrieben, die alle auf eine Fundamentalsymmetrie von sehr geringem Umfang zurückgehen, welche im wesentlichen durch die sogenannte "Konfigurationszahl" k bestimmt wird, für die es nur die Möglichkeit k=1 oder k=2 gibt. So erweist sich die aus empirischen Gründen eingeführte Baryonenladung als k-1, d.h., k=1 steht für Mesonen und k=2 steht für Baryonen.

Von einem solchen Flußaggergat im R₆ sind auf jeden Fall die Komponenten im physischen Raum R3 physikalisch relevant, deren Zahl k+1 beträgt, also zwei für Mesonen und drei für Baryonen. Hier liegt offensichtlich eine Analogie zu dem aus empirischen Gründen konzipierten Begriff der "Quarks" vor. Wenn dies so ist, dann wären die Quarks keine fundamentalen Partikel, sondern (als R₃-Komponeneten des gleichen Phänomens) die nicht trennbaren quasikorpuskulären Subkonstituenten eines mesonischen oder baryonischen Elementarpartikels. Die Bedingung eines "Confinements" wird daher in diesem Bild überflüssig. Welche Bedeutung einer evtl. Quantenchromodynamik zukäme muß sich aus einer einheitlichen Beschreibung möglicher Wechselwirkungen ergeben, was in 3 untersucht wird. Dennoch erscheint eine metrisches Feld in R₃, welches die k+1 Subkonstituenten umhüllt (Stratonfeld).

Für die Trägheitsmasse sind die als Protosimplexe bezeichneten Urelemente des Flußaggregats relevant, von denen die k+1 Subkonstituenten im R₃ strukturiert werden. Sie bilden 4 Konfiguarationszonen in einem dynamischen Gleichgewicht, so daß während der Existenzdauer eine konstante Partikelmasse meßbar ist. Versucht man hingegen (z.B. durch Neutrinostreuungen) die Masse eine Subkonstituenten zu ermitteln, dann werden sich variable sehr große Bandbreiten ergeben, weil eine solche Masse von der jeweiligen zeitlichen Flußphase abhängt. Hingegen sind aus diesem Grund die Summen der k+1 Subkonstituentenmassen stets konstant und liefern im wesentlichen die meßbare Partikelmasse. Relevant hierfür sind die Besetzungen der Konfigurationszonen durch die dynamischen Flußelemente im physischen R₃. Für k=1 und k=2 gibt es insgesmt 25 Quantenzahlensätze, die invariante Ruhemassen, also entsprechende Konfiguretionszonenbesetzungen kennzeichnen. Die entsprechenden Partikel dieser invarianten Grundmuster sind wiederum in mehreren Familien von Spinisomorphismen zusammengefaßt, und die räumliche Flußdynamik erscheint in einem dynamischen Gleichgewicht und zwar in einer Dynamik der Konfigurationszonen. In allen diesen Termen gibt es füt k=1 und k=2 jeweils eine nur von k bestimmte invariante Zonenbesetzung (Gerüststruktur) die in die Masenformel [2] eingesetzt, mit sehr guter Wiedergabetreue die Masen des Elektrons und des Protons liefern. Auch die übrigen Massen dieser Grundzustände werden in ähnlicher Qualität wiedergegeben, doch scheint die Existenzdauer eines Zustandes von der Abweichung der Konfigurationszonenbesetzung von der betreffenden Gerüststruktur abzuhängen. Auch wäre denkbar, daß es in Analogie zur organischen Chemie optisch aktiver Antipoden auch im Bereich solcher Flußaaggregate Enantiostereoisomerien gibt, die sich in Schwankungen der zeitlichen Existenzdauer äußern. Möglicherweise können so die beiden massegleichen Komponenten des K⁰-Mesons, nämlich K⁰_S und K⁰_L verstanden werden. Schließlich kann noch als Leerraumbedingung das Verschwinden aller Zonenebestzungen und des elektrischen Ladungszustandes gefordert werden, was im Bereich k=1 zu einigen Massen führt, die als Neutrinozustände interpretierbar sind. Es handelt sich hierbei jedoch weder um Ruhemassen, noch um freie Feldenergie (analog dem Photon), sondern (metaphorisch ausgedrückt) um "Feldkatalyte" quantenhafter Art, die Gruppentheoretische Eigenschaften (aus den Quantenzahlensätzen) durch den physischen R₃ transferieren.

Die in 2 hergeleitete Spektralformel hängt noch von einer positiven ganzen Zahl 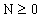 ab, wobei sich N= 0 auf die 25 Massenterme der Grundmuster bezieht. ZahlenN>0 liefern für die Quantenzahlensätze ebenfalls Massen, die auf energtische Resonanzanregungen dieser Grundmuster zurückgehen, wobei nach der Konfigurationszonendynamik für jeden wert N nur eine Zonenbestzung möglich ist. Die so entstehenden Massen geben offenbar die kurzlebigen Resonanzen wieder, denn die gemessenen Resonanzen erscheinen alle in diesen Spektren. Allerdings ist in jedem Fall N begrenzt, weil es für jeden Quantenzahlensatz x eine endliche Rsonanzgrenze 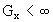 gibt, so daß für die Resonanzordnungen N (einschließlich des Grundzustandes) die geschlossenen Intervalle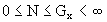 gelten.

Von der relativ großen Zahl logisch möglicher Partikelmassen wird von den gegenwärtigen hochenergiephysikalischen Experimenten an den Beschleunigern jedoch nur die verhältnismäßig kleine Untermenge derjenigen Partikel erfaßt, deren Bildungswahrscheinlichkeiten (bezogen auf die Randbedingungen des Experimentes) hinreichend hoch sind. Es fehlt offenbar noch eine einheitliche mathematische Beziehung für diese Bildungswahrscheinlichkeiten in Abhängigkeit von den Partikeleigenschaften und diesen experimentaltechnischen Randbedingungen.

Es handelt sich bei diesen Ausführungen in [1] und [2] um eine halbklassische Untersuchung, die zu einer Hyperraumdynamik im R₁₂ aus diesem halbklassischen Bereich hinausgeführt wird. Diese Schrift [3] mit dem Titel "Strukturen der physikalischen Welt und iherer nichtmateriellen Seite" befindet sich z.Zt. im Druck. Nach herausgabe kann ihr Inhalt in ähnlicher Weise diskutiert werden.

Burkhard Heim
Schillerstr. 2
D–37154 Northeim

[1] Heim, B. Elementarstrukturen der Materie, Vol. 1 (revised), Resch Verlag, Innsbruck, Austria, 1989

[2] Heim, B. Elementarstrukturen der Materie, Vol. 2, Resch Verlag, Innsbruck, Austria, 1984

[3] Dröscher, W., and Heim, B. Strukturen der physikalischen Welt und ihrer nichtmateriellen Seite, Resch Verlag, Innsbruck, Austria, 1996